How to Master Memoization in Python

In seventh and eighth grades, we were taught Sequences and Series in Mathematics. In most cases, it took several minutes (and even hours) to find the various values of a sequence. However, if you have a brilliant memory, it would take a second or less to answer when asked the value of a particular term in a sequence that you solved seven minutes ago. To our brains, this process of remembering the answer to a mathematical problem is referred to as memorization. But, when working with computers, the same is referred to as Memoization in Python. 

Well, they sound alike but the letter ‘r’ is missing in this case. 

In this article, you will understand what memoization in Python is, how to practice memoization using recursive Fibonacci in Python, and how the components of memoization works. 

So, first…

What is memoization in programming?

Memoization is a computing technique used to speed up programs. It does this by caching up the results of previous processes (calculations or functions) to be regurgitated whenever the same process is initiated. 

Just as you were asked for the answer to a math problem 4 minutes after solving the same exact problem, you can simply blurt out the answer. There’s no need to go through the rigorous calculations when you already have it upstairs. 

Though the irony is in the naming. You might easily conclude that it was coined from misspelling “memorization.” Actually, it wasn’t.  In 1968, Donald Michie fabricated the term from the Latin word “memorandus” (plural of memorandum) which literally means “to be remembered.” 

Well, that makes sense. If a computer function is to be remembered, there’s no harm in saying that it should be memoized. 

Using recursive Fibonacci in Python to explain memoization. 

Like all recursive functions, a recursive Fibonacci sequence is a function defined by terms of itself through self-referential expressions. An example of recursive Fibonacci sequence is: 

Isn’t this sequence familiar? The third term of the Fibonacci sequence above is the sum of the second and first terms. The fourth is the sum of the third and second. So, the formula n =(n-1) + (n-2) holds true at any point along the sequence. 

If you are asked, for instance, to calculate the 48th term of this sequence above, you would have to compute the values of the 46th and 47th terms first. Isn’t that right? 

What would you do if you had solved for the 46th and 47th terms on the previous page of your math notebook? You would simply flip over to get the values and sum it right up to deduce the 48th term. Easy peasy! 

For computer programs running on Python, the same thing happens. If it had, at any point, processed the 46th and 47th terms of this sequence above and cached the answers, it doesn’t have to go through the time-consuming troubles of solving for them first before solving for the 48th term which you are trying to find. 

The process of storing these function calls (also known as process results) in its dictionary (more like its brain) is referred to as caching in Python. But let’s dive a little deeper. 

How does caches work in Python?

Programs can run a function call afresh every time it is required. With all things being equal, it would take exactly the same time to process the function call every time if the first process was not cached. 

This means that if it takes a computer program 47 seconds to compute the 187th term of that recursive Fibonacci sequence above, you will have to wait 47 seconds every time you input that “n = 187” function. 

However, if the cache function is included in the program’s coding, it would take 47 seconds the first time you make that function call. Every other time after that one will happen in a few microseconds.

To ensure that your program caches function calls, you must include the cache instruction in your code. Let’s revisit that recursive sequence one more time. 

To write a default Python code that automates the function calls on this sequence, you can use the code below.

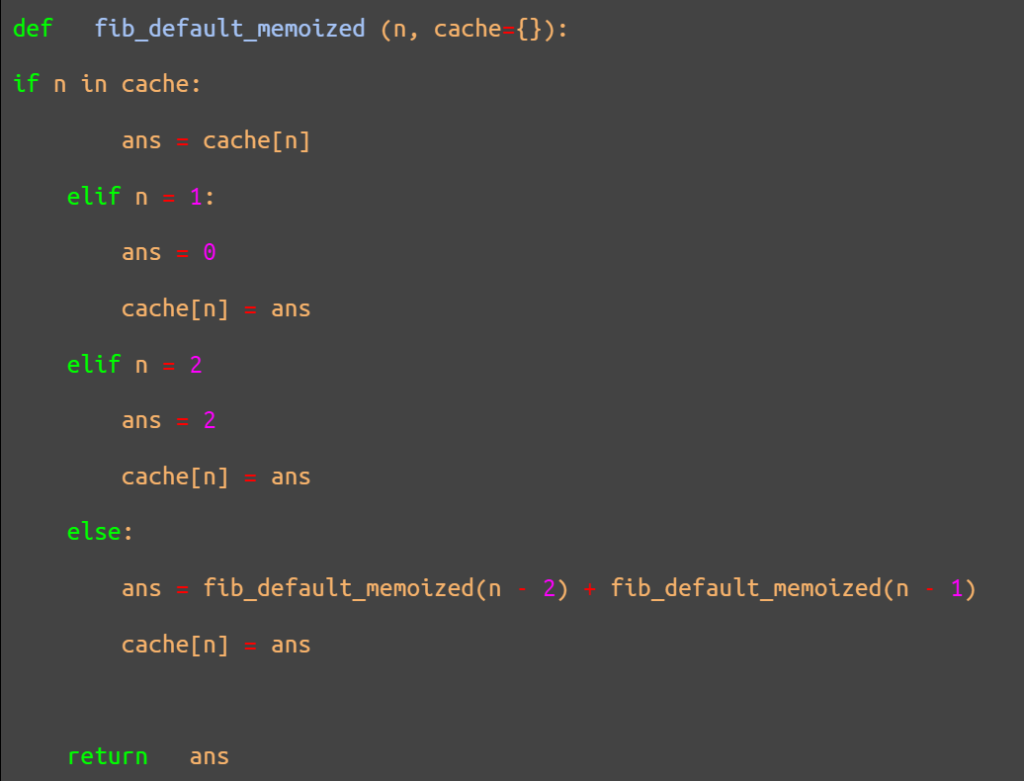
Now, let’s break down this code, starting with the first line.

This line defines the function being called. In this case, it is the default Fibonacci sequence memoized and cached for every previously computed value of n. The “{}” is the dictionary, the theoretical brain of the program that stores previous function calls. In this code, it is empty. It fills up with values after every new function is called to compute novel values for n. 

Moving on to the second part of the code: 

This part of the code comes to effect if the value of n being called has been computed and cached before. It instructs the program to simply display the cached answer for that imputed call. 

The third part:

This set of codes reminds the program that the values of the first and second terms of the sequence are 0 and 2 respectively. Also, that there is no need to try to compute it. So, simply cache the answer and bring it up whenever the user wishes to know the value of n = 1 or n = 2. 

This fourth part of the program becomes effective only if the second and third parts do not satisfy the query. That is if the value of n has never been computed and cached before (part two function) and the value of n is neither 1 nor 2. 

This function triggers the program to solve for the value of the nth term by pulling and summing up the values of (n-2) and (n-1) from the cache of which their n values will be contained within the “{ }” in the first line. 

The more values it has to compute to arrive at the final result for the queried nth value, the longer it would take the program to complete the function call. When an answer is finally reached, the “cache[n] = ans” instruction sends the result to the cache dictionary to be pulled up at a later time, upon request. 

The last line instructs the program to display the final answer for the user to see. 

Dealing with factorials in Python

Python factorials (!) are similar to the factorial rule of the combination and permutation formulae of mathematics. If the factorial of a value is called, Python programs automatically multiply that value with every number succeeding it in decimal order. 

That is:

7! = 7x6x5x4x3x2x1 =5,040

6! = 6x5x4x3x2x1 = 720

5! = 120

4! = 24

3! = 6

2! = 4

1! = 1

These functions can be reframed as:

7! = 7×6!

5! = 5×4!

Therefore, if the program already had the value of 6! cached, it would return a function call for 7! faster. However, if the first next function call after that is for 23!, it would take a bit longer as it solves for every uncached value leading up to 23. And it would cache each of those values as it processes them to call them up whenever they are needed in a later time. 

Conclusion

Several programs use memoization to speed up function calls and provide instant returns for queries right after you hit the enter button. Virtually every website that you visit is storing caches on your device to help it deliver a faster experience to you through memoization so that you don’t have to wait to redo every request. 

We hope that this explanation was comprehensive enough and you could master memoization in Python with due practice. Join the SDS Club to practice and learn alongside hundreds of other data scientists and slo prepare for career changing tests.

Don’t forget to share this article with your friends on social media. And Subscribe to our newsletter to stay up to date on data science topics and trends.